
Data SA
Data:
Data are simply values or sets of values. A data item refers to a single unit of values. Data items that are divided into sub items are called group items. Data items that are not divided into sub items are called elementary items.
Data Structure:
The logical or mathematical model of a particular organization of data is called data structure.
Array:
Array is a finite set of ordered, homogeneous element.
Algorithms:
Algorithm is an well – defined set of list of steps for solving a problem.
Linear Data Structure:
A data structure is said to be linear if its elements form a sequence or linear list. There are two basic ways to represent the structure in memory. Here the elements are traversed sequentially starting from the beginning.
(1) linear relationship between the elements in represented by means of sequential memory location. eg: Array.
(2) linear relationship between the elements is represented by means of pointers and links. eg: Linked list.
Nonlinear Data Structure:
They are used to represent the data of hierarchical relationship between elements. Here the elements are not traversed sequentially, rather they are traversed in a non-linear fashion. Eg: graphs and trees. In case of trees we have to start from root but we have to traverse either left subroot or right subroot, but not the both.
Big OH notation:
Let, f (n) and g (n) B two non-negative functions. The function f(n)= o(g(n)) (read as & of n equals big-oh of n) If there exist two constants c & no such that |f(n)| ≤ c * |g(n)| for all n>no.
- F(n) will normally the computing time of some algorithm. When we say that the computing time of an algorithm is o(g(n)), we mean that execution time is no more than a constant time g(n), where is a parameter which characterizes as input/output.
- Ω notation: – Let f (n) and g (n) be non-negative functions. Then the function f (n)= Ω (g(n)) (read as f of n equals ℰomega of g of x) there exist two c& no such that
|f(n)|≥ c* g (n) for all n ≥ no
-
– notation: – f (n) =
(g(n)) if f there exist three constants c1,c2 & no such that
|c1 g(n)| ≤ f (n) ≤ |c2 * g (n)| for all n ≥ no
Abstract data type:
Abstract data types are set of values and associated operations that are precisely independent of any particular implementation. The strength of an ADT is that, the implementation is hidden from the user, only interface in declared. This means, that ADT can be implemented in various ways, but as long as it adheres to the interface, user program is an affected. Stacks and Queues are the examples of ADT. Stack defines an interface, which consists of data and operations PUSH & POP. These operations are abstract in the sense, they are declared only, no implementation is provided with them. Queues also have such abstract methods like INSERT and REMOVE without any implementation.
Properties of algorithm: –
(1) Input: Each algorithm is supplied with a zero or more external quantities.
(2) Output: Each algorithm must produce at least one quantity.
(3) Definiteness: Each instruction must be clear and unambiguous
(4) Finiteness: The algorithm must terminate after a finite no. of steps within finite
time.
(5) Effectiveness: Each instruction must be sufficiently basic and also be feasible.
Various operations on data structure: –
(1) Traversing: also called visiting means accessing the required record to process
Data.
(2) Searching: finding the location of record to be processed.
(3) Inserting: adding a new record to structure
(4) Deleting: Removing record from structure
(5) Sorting: arranging the record in some logical order.
(6) Merging: combining too different sets of records to form a final set of record.
Time complexity of an algorithm:
The amount of time the computer requires to execute a program.
Space complexity of an algorithm:
The amount of memory space, the computer requires, completing the execution of algorithm
Static memory allocation:
In case of static memory allocation, memory is allocated during the compile time of program.
Arrays are the most fundamental data structures used of storage but the size of the array cannot be changed during execution of program. Hence arrays are static memory allocation scheme
Dynamic memory allocation
In case of this memory space for any variable is allocated during the time of execution. Hence memory can be created and destroyed during execution time of program.
Linked list are dynamic memory allocation scheme.
STACKS AND QUEUES
Stack: Stack is an abstract data type in which insertion and deletion can take place only at one end, called the top.
Stack is also called LIFO (Last In First Out)
Basic operations of stack
Our stacks will be maintained by a linear array STACK, a pointer variable top which contains the locator of the top element of stack. and a variable MAX which gives the max number of elements that can be held by stack. The condition TOP = -1 will indicate that the stack is empty.
The procedure PUSH pushes an item onto a stack.
PUSH (STACK, TOP, MAX ITEAM)
- Step 1: [ stack already filled?]
if TOP == MAX, then print: Overflow, and return.
- Step 2: Set TOP = TOP + 1 (Increases TOP by 1)
- Step 3: Set STACK[TOP] = ITEM (Inserts item in new TOP position)
- Step 4: Return.
The procedure POP deletes the TOP element from STACK and assigns it to variable ITEM.
POP (STACK, TOP, ITEM)
- Step 1: [Stack has an item to be removed?]
if TOP = -1, then print: Underflow and return.
- Step 2: Set ITEM = STACK[TOP]
(Assign TOP element onto STACK)
- Step 3: Set TOP = TOP – 1 (Decreases TOP by 1)
- Step 4: Return.
Algorithm of transforming infix to postfix: –
Suppose Q is an expression written in infix notation. The following algorithm finds the equivalent postfix expression P.
- Step 1: Push ‘(‘ onto stack and add ‘)’ to Q.
- Step 2: Scan Q from left to right and repeat step III to step VI for each element until the stack is empty.
- Step 3: If an operand is encountered, add it to P.
- Step 4: If a left parenthesis is encountered, push it to stack.
- Step 5: If an operator X is encountered,
(a) then repeatedly pop from stack and add it to P from the top of the stack, if it has the same precedence or higher precedence than the operator X.
(B) Add the operator (X) to stack.
- Step 6: If right parenthesis is encountered, then
(a) Repeatedly Pop from stack and add to P until a left parenthesis is encountered.
(b) Remove the left parenthesis and do not add it to P.
End of step 2 loop.
- Step 7: Exit
Algorithm for Evaluation of Arithmetic Expressions
Suppose (P) is an arithmetic expression written in postfix form. The following algorithm gives the value of the arithmetic expression.
- Step 1: Add a right parenthesis to p.
- Step 2: Scan (P) from left to right and repeat Step 3 & 4 for each element until the right parenthesis is encountered.
- Step 3: If an operand is encountered, push it onto stack.
- Step 4: If an operator (×) is encountered,
(a) Pop the top 2 elements of stack where A is the top element & B is the next to top element.
(b) Evaluate B × A.
(c) Place the result of (b) back to stack.
- Step 5: Set VALUE = top element of stack.
- Step 6: Exit.
Conversion of Infix to postfix:
A + (B * C – (D / E ^ F) * G) * H)
| Symbol Scanned | Stack | Expression P |
| ( | ||
| A | ( | A |
| + | (+ | A |
| ( | (+( | A |
| B | (+( | AB |
| * | (+(* | ABC |
| – | (+(- | ABC* |
| ( | (+(-( | ABC* |
| D | (+(-( | ABC*D |
| / | (+(-(/ | ABC*D |
| E | (+(-(/ | ABC*DE |
| (+(-(/ | ABC*DE | |
| F | (+(-(/ | ABC*DEF |
| ) | (+(- | ABC*DEF |
| * | (+(-* | ABC*DEF |
| G | (+(-* | ABC*DEF |
| ) | (+ | ABC*DEF↑/G*- |
| * | (+* | ABC*DEF↑/G*-H |
| H ) | (+* | ABC*DEF |
Queue: A queue is an abstract data type in which the elements are placed in a list and one end of the list is designated as the front and the other end is designated as the rear. The elements are removed from the front end of the list and inserted at the rear end. Queue is also called FIFO (First In First Out).
Deque: Deque is an abstract data type in which elements can be inserted or removed at either but not in the middle. This is also called Double-ended queue.
There are two variations in deque.
(i) Input Restricted deaque: which allows inspections only ne end of the list but deletions at both ends of the list.
(ii)output restricted deque: which allows deletions only one end but instructions at both ends of the list.
Since both insertion and deletion can be performed from either end, there will be four different insertion & deletion operations:
(i) Insertion of an element at the rear end of queue
(ii) Insertion of an element at the front end of queue
(iii) Deletion of an element at the rear end of queue
(iv) Deletion of an element at the front end of queue
Let us assume, dqueue[ ] (dimension length N) is an array, which will be used for dequeue. R & F are the two variables to store the positions of the rear and front elements of dqueue[ ]. R & F are declared globally.
- Function for inserting an element at rear end:
void insert_re(int x)
{
if (R == N)
printf (“Queue is full”);
else
{
R++;
dqueue[R] = x;
}
return();
- Function for inserting an element at front end:
void insert_fr(int x)
{
if (F == 0)
printf (“Queue is full”);
else
{
F= -;
dqueue[R] = x;
}
return();
}
- Function for deleting an element at front end:
void insert_fr(int x)
{
if (F == 0)
printf (“Queue is full”);
else
{
F=-;
dqueue[F] = x;
}
return();
}
- Function for deleting an element at front end:
int delete_fr()
{
if (F == R) {
printf (“Queue is empty”);
else
{
y = dqueue [F];
F++;
return (y);
}
- Function for deleting an element at rear end:
int delete_re()
{
if (R == F) {
printf(“Queue is empty”);
} else {
int y = dqueue[R];
R–;
return y;
}
return 0;
}
Priority queue: A priority queue is a collection of elements such that each element has been assigned a priority and such that the order in which the elements are deleted and processed comes from following rules:
1. An element of higher priority will be processed before any element of lower priority.
2. Two elements of the same priority will be processed according to the order in which they were added to the queue.
One-way list representation of priority queue:
To maintain priority queue in memory, one-way list is used-
(1) Each node in the list will contain three items information’s; an information field INFO, a priority number PRN, and a link number LINK.
(2) A node X precedes a node Y in the list (a) when X has higher priority than Y, and (b) when both have the same priority, but X is added to the list before Y. This means that the order of a one-way list corresponds to the order of priority queue.
Circular queue: Suppose we want to insert an element ITEM to a queue at the time when the queue does occupy the last part of the array i.e., REAR = N. One way to do this is to move the entire queue to the beginning of the array, changing REAR & FRONT accordingly, and then inserting the ITEM.
This procedure may be very expensive. So, we adopt a procedure by which Queue [1] comes after Queue [N] in the array. With this assumption, we insert ITEM to a queue [1]. Specifically, instead of increasing Rear to N+1,we reset REAR =1 and then assign.
Queue[Rear] = ITEM;
Similarly, if FRONT = N, and an element of QUEUE is deleted, we reset FRONT = 1 instead of increasing FRONT to N + 1. As the process is done in a circular fashion, the queue is called circular queue.
Queue insertion:
Void insert (item)
{
if (R == N)
{
printf(“Queue is full”);
}
else
{
queue[R] = item;
}
}
Algorithm of queue insertion:
- Step1: If Rear = N, then print “OVERFLOW” and return.
- Step2: Set REAR = REAR + 1
- Step3: Set queue[REAR] = ITEM
- Step4: Return.
- Function of queue deletion:
int delete()
{
int j = 0;
if (front < 0 || front > rear)
{
printf(“queue is empty”);
}
else
{
f = f + 1;
j = queue[f];
}
return (j);
Algo:
- Step1: If FRONT < 0 or FRONT > REAR, then print “queue is empty” and return.
- Step2: Set FRONT = FRONT + 1.
- Step3: Set j = queue[FRONT].
- Step4: Return.
- Circular queue Insertion:
Cir-inser (queue, item)
{
if (rear + 1) % max_size_of_queue == front)
{
rear = (rear + 1) % max_queue_size;
queue[rear] = item;
}
else
{
printf(“Queue is full”);
}
Circular queue deletion:
Cir-delete (queue, item)
{
if (front == rear)
{
printf(“Queue is empty”);
else
{
front = (front + 1) % Max_queue_size;
item = queue[front];
}
return (item);
}
Difference between stack and queue
| Features | Stack | Queue |
| Insertion | Here items are inserted at the end of an array or a linked list. | Here items are inserted at the end of an array or a linked list |
| Deletion | Here items are deleted from the end of an array or a linked list. | Here items are deleted from the beginning of an array or a linked list. |
| Variables/pointers used | It uses a variable or pointer Top, which keeps the track of stack top. Top is incremented when items are inserted & is decremented when items are deleted. | It uses two variables or pointers, Rear & Front. Rear is incremented when items are inserted & Front is incremented when items are deleted. |
| Usage | in DFS traversal of graph | in BFS traversal of graph |
| Type of Data Structure | LIFO | FIFO |
Finding factorial using recursion:
Factorial (Fact, N)
This procedure calculates N! and returns the value in the variable Fact.
- Step1: If N = 0, set Fact = 1 and return.
- Step2: Call Factorial (Fact, N – 1)
- Step3: Set Fact = N * Fact.
- Step4: Return.
.
Fibonacci using recursion:
FIBONACCI (FIB, N) This procedure calculates Fn and returns the value in the first parameter FIB.
- Step1: If N = 0 or N = 1, set FIB = N and return.
- Step2: Call FIBONACCI (FIBA, N – 2)
- Step3: Call FIBONACCI (FIBB, N – 1)
- Step4: FIB = FIBA + FIBB
- Step5: Return.
Definition of Fibonacci Sequence:
The discrete Fibonacci sequence is as follows:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
i.e. F0 = 0, F1 = 1, and each succeeding term is the sum of the two preceding terms.
A formal definition of Fibonacci:
1. If n = 0 or n=1, Fn = n
2. If n > 1, Fn = Fn-2 + Fn-1
Recursive solution of Towers of Hanoi
TOWER (N, BEG, AUX, END)
This procedure gives a recursive solution to the Towers of Hanoi problem for N disks.
- Step1: If N = 1, then (a) write BEG → END (b) return.
- Step2: [Move N-1 disks from BEG to AUX] call TOWER (N-1, BEG, END, AUX)
- Step3: [Move N-1 disks from beg AUX to beg END] call TOWER (N-1, AUX, BEG, END)
- Step4: Return.
TREES
1. Degree of a node: The number of subtrees of a node is called the degree of that node.
– e.g. the degree of A is 2.
– The degree of H is 0.
The number of nodes connected by link to a given node n is called the degree of that node n.
– e.g. the degree of B is 3.
– The degree of H is 0.
2. Terminal or Leaf node: Such node which does not have any children is called leaf node.
– e.g. D, F, H, G are leaf nodes.
3. Degree of tree: The degree of a tree is the maximum degree of nodes in a tree.
– e.g. here degree of tree is 2.
4. Siblings: Children of same parents called Siblings.
5. Level: The level of the node is defined by assuming root is at level zero. [Some books consider root as level 0]. If a node is at level p, then its children are at p+1 level.
6. Depth or height of tree: Depth or height of a tree is defined as the maximum height of any node in the tree.
7. Ancestors: Ancestors of a node are all the nodes along the path from root to that node. e.g. Ancestors of node H are C and F.
8. Binary tree: Binary tree is a tree in which the degree of each node is less than or equal to 2. i.e. the tree can have 0, 1, or 2 children.
*An empty tree is also a binary tree.
9. Strictly binary tree: A strictly binary tree is a binary tree in which the degree of each node is either zero or two.
10. Complete binary tree: A complete binary tree is a strictly binary tree in which the number of nodes at any level ‘i’ is 222-1, assuming root at level 1. If level is at zero, the number of nodes at any level ‘i’ is 22.
11. Binary Tree Traversal:
There are three ways of traversing a binary tree:
- Preorder: Root (N) → Left → Right
- Inorder: Left → Root → Right
- Postorder: Left → Right → Root
Example: For the given tree:
23
/ \
18 24
/ \ \
12 20 25
/ \ \
2 8 54
- Preorder: 23, 18, 12, 2, 8, 20, 24, 25, 54
- Inorder: 2, 12, 8, 18, 20, 23, 24, 25, 54
- Postorder: 2, 8, 12, 20, 18, 54, 25, 24, 23
12. Non-recursive algorithm for Inorder Traversal:
The algorithm uses a variable PTR, which will contain the location of the node N currently being stacked. The algorithm uses a stack, which will hold the address of the nodes for future processing. Initially push NULL onto the stack and set PTR = root. Then repeat the following steps until PTR = root.
- Step1: Proceed down the left most path rooted at PTR, processing each node N on the path and pushing the right child R(N) onto stack. The traversing ends after a node N, with no left child, is processed.
- Step2: (backtracking) Pop and assign to the PTR, the top element of the stack. If PTR ≠ NULL then return to step (1), otherwise exit.
13. Non-recursive algorithm of Inorder Traversal:
Initially push NULL onto stack and set PTR = root. Then repeat the following steps until PTR = NULL.
- Step(1): Proceed down the left most path rooted at PTR, pushing each node into stack and stopping when a node N having no left node child is pushed onto stack.
- Step(2): Pop and process the nodes on stack. If null is popped then exit. If a node N having right node R(N) is processed, set PTR = address of R(N) and return to step (1).
14. Non-recursive algorithm of Postorder Traversal:
Initially push NULL onto stack and set PTR = root. Then repeat the following steps until PTR = NULL.
- Step(1): Proceed down the left most path rooted at PTR. Push N and stop if N has a right child R(N), then push-R(N) onto stack.
- Step(2): Pop and process the nodes from stack. If NULL is popped then exit. If -ve node
is popped, if PTR = – R(N), set PTR = N and return to step 1.
15. Searching in Binary Search Trees:
FIND(INFO, LEFT, RIGHT, ITEM, PAR, LOC, ROOT)
A binary tree T is in memory and an ITEM of information is given. This algorithm finds the location LOC of item and the location of parent PAR of ITEM. There are three special cases: –
- If a LOC = NULL and PAR =NULL will indicate that the tree is empty.
- LOC≠ NULL and PAR = NULL will indicate that the ITEM is the root of tree.
- LOC=NULL and PAR≠ NULL will indicate that the ITEM is not in the tree.
- Step 1: If ROOT = NULL, then set LOC = ROOT and PAR = NULL and return. [Tree empty]
- Step 2: If ROOT ≠ NULL, then set LOC = ROOT and PAR = NULL and return. [Item of root?]
- Step 3: [Initialize pointers PTR and SAVE]
If ITEM< INFO [ROOT],
Set PTR = LEFT[ROOT] and SAVE = ROOT.
else
Set PTR = RIGHT[ROOT] and SAVE = ROOT.
[End of if structure]
- Step 4: Repeat step 5 and 6 while PTR ≠ NULL.
- Step 5: If ITEM < INFO[PTR], then set LOC = PTR and PAR = SAVE and return.
- Step 6: If ITEM < INFO[PTR], then
Set PTR = LEFT[PTR] and SAVE = PTR.
else
Set PTR = RIGHT[PTR] and SAVE = PTR.
[End of if structure]
[End of step 4 loop]
- Step 7: [Search unsuccessful]
Set, LOC=NULL and PAR = SAVE
- Step 8: Exit
16. Algorithm for insertion of ITEM into a BST:
1. TREE (Root, newnode)
The following algo inserts a new node with a DATA part in proper place. If the tree is non-empty, then compare the DATA with the DATA of the Root of the tree, which is already created.
- Step 1: Repeat step 2 until ROOT = NULL.
- Step 2: if new node → DATA < ROOT → DATA then,
if ROOT → LEFT = NULL then
step (a): set ROOT → LEFT = newnode.
step (b): set ROOT = NULL.
else:
ROOT = ROOT → LEFT
[end of inner if]
else:
if ROOT → RIGHT = NULL then
step(a): set Root → RIGHT = Newnode
step(b): set Root = NULL
else:
Root = Root → RIGHT
[End of inner if]
[End of outer if]
[End of step 1 loop]
17. Algorithm of deletion from a BST:
To delete an item node with DATA from a binary search tree, there are three cases to consider.
- Case 1: Deletion of the node having no child
- Case 2: Deletion of a node which has exactly one child
- Case 3: Deletion of a node which has two children
Suppose a binary search tree and an item is given. The algorithm first finds the location of node N which contains ITEM and the location of the parent node (PN). The way N is deleted from the tree depends on the no. of children of node N.
- Case 1: N has no children, then N is deleted from BST. by simply replacing the location of N in parent node (PN)
by NULL pointer.
- Case 2: N has exactly one child. Then N is deleted from T by replacing the location of N in parent node (PN) by the location of the only child of N.
- Case 3: If N has two children, the (SCN) denotes the inorder successor of N. N is deleted from T by first deleting (SCN) from T by using case 1 or case 2 and then replacing node N by the node (SCN).
18. Recursive Algorithm of Preorder traversal:
Let ptr-root be the address of root node of the tree. The function Preorder recursive (Ptr-ROOT) contains the parameter of address of root of the root node. If ptr-ROOT! = NULL
- Step 1: Print,ptr Root
info
- Step 2: Traverse the left subtree of the ptr-ROOT in preorder i.e. call the function Preorder recursive with the parameter ptr ROOT ptr
LEFT.
- Step 3: Traverse the right subtree of the ptr-ROOT in preorder i.e. call the function Preorder recursive with the parameter of ptr-ROOT → RIGHT.
19. Recursive algorithm of Inorder Traversal:
Let ptr-ROOT be the address of the root node of the tree.
If ptr-ROOT! = NULL
- Step 1: Traverse recursively through the left subtree by calling the function Inorder underscore Recursive (ptr-ROOT → LEFT).
- Step 2: Print,ptr Root-> info
- Step 3: Traverse recursively through the right subtree by calling the function Inorder underscore recursive (ptr-ROOT → RIGHT).
20. Recursive Algorithm of Postorder Traversal:
Let ptr-ROOT be the address of the root node of the tree. If ptr-ROOT != NULL
- Step 1:
Traverse the left subtree of the root node in postorder i.e. call the function Postorder_recursive with the parameter ptr-ROOT -> LEFT.
- Step 2:
Traverse the right subtree of that root in postorder i.e. call the Postorder_recursive with the parameter ptr-ROOT -> RIGHT.
- Step 3:
Print ptr-ROOT -> INFO.
21. Definition of Binary Search Tree:
A binary search tree is a binary tree which is either empty or else it inserts every node containing data satisfies the following conditions:
1. The data of left child of a root node is less than the data of the root node.
2. The data of right child of a node is greater than the data of its parent node.
3. The left and right subtrees of root node are binary search trees.
22. AVL Trees:
AVL Tree is also called Height balanced binary search tree. It is called Depth or height of a binary tree is the max. level of the levels leaves. The height of a NULL tree is defined as -1. A balanced binary search tree which is called AVL trees is a binary search tree in which the heights of two sub trees of every node do not differ by more than 1. The balance of a node in a binary tree is defined as the height of its left subtree minus height of its right subtree.
Balanced Factors |HL-HR|:
Case R-R: Only required left rotation about unbalanced node.
Case L-L: Only required right rotation about unbalanced node.
Case R-L: Required rotation about immediate successors of unbalanced node.
1. Do the left rotation about unbalanced node.
2. Left rotation about immediate successor of unbalanced node.
Case L-R: Do the right rotation about unbalanced node.
23. B-tree (Binary Balanced Sort Tree)
A B-tree of order m is an m-way tree in which
1) All the leaves are on the same level
2) All internal nodes except the root have at most m non-empty children and at least ⌈m/2⌉ non-empty children.
3) The root, if it is not a leaf, has at least two children.
4) The number of keys in each internal node is one less than the number of its children and the keys partition the keys in the children in the fashion of a search tree.
If the root has at most two children, the tree consists of a root alone.
Prove that the maximum no. of nodes in a binary tree of depth h is 2^(h+1) – 1.
The max no. of nodes in a binary tree of level i is 2^i. (Assuming root at level 0)
Hence the no. of nodes in a binary tree of depth h is the summation of max no. of nodes from level 0 to level h.
∑ (i=0 to h) 2^i = 2^(h+1) – 1
For any non-empty binary tree, T, if n0 be the number of terminal nodes and n2 be the number of nodes of degree 2, then n0 = n2 + 1.
Prove it
Let n be the number of nodes of degree 1, and T be of degree less than or equal to 2. Since all nodes of T are of degree less than or equal to
Then, n = no+n1+n2-(i)
If we count the number of branches in a binary tree, we see that all nodes except the root has a branch leading into it. If B is the number of branches, then n = B + 1 –(ii)
All branches emanate either from a node of degree 0 or a node of degree 2. Then,
B = n1 + 2n2 ……….(iii)
From (i) and (iii), we can write
n = n1 + 2n2 + 1 ……….(iv)
From (i) and (iv), we get
n0 = n2 + 1 [Proved]
GRAPHS
24. Graph: –
Graph is a non linear data structure. Mathematically, graph can be defined as G = (V, E)
where V = finite and non-empty set of vertices and E = set of edges which are the pair or set of vertices. Eg: v =1,2,3,4 & e={<1,2>,<1,3>,<2,4>,<4,3>}
25. Undirected Graph:-
A graph which has unordered pair of vertices is called undirected graph. The edges have no direction. Hence we can write (Vi, Vj) & (Vj, Vi) are equal.
26. Directed Graph:-
A graph in which each edge is represented by an ordered pair of vertices is called directed graph. In directed graph, the set elements called edges are written as ordered pair (Vi, Vj) and (Vi, Vj) represent two different edges. So the verticles are{1,2,3,4} and edges are {<1,2>,<2,3>,<3,4>,<4,1>,<3,1>}
Directed graph is also known as diagraph.
27. Degree:-
Degree of a vertex means the summation of indegree and outdegree of that vertex. Indegree of a vertex in a graph is the number of edges coming to that vertex and outdegree is the number of edges going outside of that vertex.
28. Incidence Matrix:-
Let G be a graph with n vertices and e edges defined by v*e whose v rows correspond to v verticels and e column correspond to e edges.
M = [mij] where: mij = 1 if ith edge ej is connected on ith vertex
otherwise mij = 0.
29. Adjacency Matrix:-
Suppose G is a graph with n nodes and e edges. Then aij = 1 if there is an edge from node i to j, otherwise aij = 0.
Such a matrix which contains 1&0 is called Bit Matrix or Bodean Matrix. The adjacency of an undirected simple graph is called Symmetric. This also means that only the upper triangle or lower triangle is sufficient to represent the graph.
All the diagonal element is zero for adjacency matrix.
If in case of directed graph aij = 1, then there is an edge from vertex vi to vj.
30. Adjacency List:- Sometimes we represent a graph using linked list. The adjacency list of the entire graph is the adjacency list for each vertex in that graph.
It generally uses less memory when a large no. of vertices and a small no. of edges remain in a graph. The total no. of nodes in an adjacency list for undirected graph having n vertices and e edges is (n + 2e). Same for directed graph is (n + e).
31. Adjacency List:-
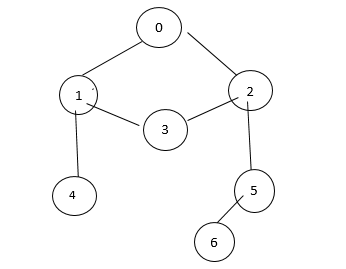
Vertex V0 : 1 2
Vertex V1 :- 2 3
4
Vertex V3 :- [1] [2]
Vertex V4 :- [1] [5]
Vertex V5 :- [2] → [4] [6]
Vertex V6 :- [5]
32. Spanning tree:-
A spanning tree of a graph is an undirected graph consisting of all the vertices necessary to connect all the nodes of the original graph.
33. Algorithm for Breadth First Search (BFS):-
- Step1:- Select a vertex S to start the traversal. Set all the vertices to zero and insert S (starting node) in queue and change the value of S to 1 as it is a visited vertex.
- Step2:- Delete the node from queue and visit all the adjacent non visited of that node insert to queue and push all vertices of A that have value zero and change it to.
- Step 3: – In BFS (j)
For call the vertices j of the graph
- Step 4: ————–visited [j] = 0;
- Step 5: In insert (j)
- Step 6: visited [j] = 1;
- Step 7: while (the queue is not empty)
{
- Step 8: N= delete ()
- Step 9: For (all the adjacent verticles J of N)
If (visited [j]==0)
{
In insert (j);
Visited [j]=1;
}
}-// End of while;
}-// End of function.
34. Algorithm for Depth First Search (DFS):-
In this traversal we use stack. Initially, we set all the vertices to zero. Push starting vertex S onto the stack and change its value to 1. Delete the top node N from the stack. Now push all the adjacent neighbours of N onto the stack which have value zero, change it to 1 and continue the procedure until the stack is empty.
- Step1:- In DFS (S);
- Step2:- for (all vertices j of the graph)
- Step3:- visited [j] = 0;
- Step 4: fn PUSH (S);
- Step 5: Visited [S] = 1;
- Step 6: While (stack b not empty) {
- Step 7: N = fn POP (S);
- Step 8: for (all the neighbours j of N)
- Step 9: if (visited [j] == 0)
{
fn PUSH (j);
visited [j] = 1;
}
} // end of while
} // end of function.
HASHING
35. Hashing:-
It is a technique whereby item or items are placed in a structure based on key-to-address transformation.
36. Uses of Hashing:-
1) Perform optimal searches and retrieval of data at a constant time i.e. O(1).
2) Increases speed, improves retrieval, optimizes searching and reduces overhead.
37. Hash Table:-
A hash table or a hash structure where we use a random-access data structure such as an array and a mapping function i.e. hashing of key to allow constant time access.
38. Hash Function:-
Hash function is a mapping between a set of input values and a set of integers, known as hash values. It is usually denoted by h.
39. Hash of key:-
If H be a hash of x and k is a key, then h(x) is called a hash of key. The hash of key is the index at which a record with the key value k must be kept.
40. Different types of hashing Methods:-
(1) Division Remainder Method:- In this method, the key element is divided by an appropriate number, generally a prime no. and the remainder of division is used as the address of record.
H(K) = K Mod M (definition) or H(K)=Hash function
K -> Key, M -> Size of the table (prime no.)
Let us consider an array of elements such as 89, 18, 49, 58, 9 and M=8.
H(K) = K Mod M
Taking the elements as key and size of the array as 8. Thus K=89 and M=8
H(89)=89 Mod 8 = 5, so 89 will be placed in location 5.
Next, 18.
H(18)=18 Mod 8 = 4, so 18 will be placed to location 4.
(2) Mid square Method:- The key K is squared. Then the H(K) = K2
Let us consider the element 1 in our previous example, H(K) = 1^2 = 1
We consider the 1st digit e.g. 1^2 = 1 indicates the element 1 will be in address 1 of the array.
41. Collision:-
A collision between two keys occurs when K1 & K2 occurs when both have to be stored in a hash table and both hash to same position address in the array.
Let us consider the following elements 89, 18, 58, 49, 29, 9
H(89) = 5 (using Division-remainder method)
H(18) = 4
H(58) = 2
H(49) = 1
H(29) = 5
H(9) = 1
Now, here already there is one element in the position 2, which is 58 in our example. But 9 is
also hashed to position 2, which is occupied by 58 in our ex. When this kind of situation occurs we say that a collision has taken place.
42. Various Collision Resolution Schemes:-
1) Open addressing:- In a general collision resolution scheme for a hash table (handling of collision), all entries of the hash table are checked until an empty position is found.
The different types of open addressing schemes are:
(i) Linear probing (sequential probing)
(ii) Quadratic
(iii) Double Hashing (rehashing)
2) Chaining:- It is a collision resolution scheme to avoid collisions in a hash table by making use of an external data structure. A linked list is often used. Instead of hashing functional value to a position, we use it as an index into an array of pointers. Each pointer accesses one entry of the element having the same location.
43. Linear Probing:-
It is one method for dealing with collisions. If an element hashes a location in hash table which is already occupied, then the table is searched sequentially from that location until an open location is found. Taking the previous examples:-
| 58 | 9 | 18 | 89 | |
Here 9 also counts the location, which is already occupied by 58, thus the next free space is 2, so 9 is adjusted the collision. Thus by sequential search we can find that 3 is the location.
So, 9 is in address 3.
44. Quadratic Probing:-
This is similar to linear probing except that the gap between places in the sequence increases quadratically.
Let D be the location at which collision occurs, then the next free space is calculated by:
D+12
Then D+22
Then D+ i2.
45. Double hashing:-
With this method, the collision is resolved by searching the table for an empty place given at intervals given by a second hash function.
h(K) = (K + c) mod M,
Where C is a second harsh function.
For the previous example, by double hashing method we compute another hashing function to adjust the value of 9. Let us consider that additional hash function as,
C= H(K)=9 MOD 5=H(9)=4
Thus C=4.
Applying double hashing,
h(K) = (K +c) mod 7 = (9+4) mod 7=6
Thus, 9 can be adjusted at location 6. The second hash function can be chosen by following these criteria:
1. It must not be the same as primary hash function.
2. It must never output a 0.
46. Clustering:-
Clustering in the hash table occurs when filled sequence in hash table becomes longer. It means that positions are occupied by elements and we have to search a longer period of time to get an empty cell. The fig. below shows a cluster in hash table. When a hash table becomes full, it means that clusters are longer. Clustering can result in longer probe lengths. This means that it is very slow to access cells at the end of the sequence. The fuller the hash table, the more clustering becomes. For example, if critical cluster designing a hash table to ensure that it never becomes more than half full, it never two-thirds full. The phenomenon is served as linear probing. This is also known as primary clustering.
Quadratic probing eliminates primary clustering. Quadratic probes differ from different clustering problem. This occurs because the key that hash to a particular cell follows the same sequence in trying to find a vacant space.
29, 11, 23, 47
Let’s say 29, 11, 23, 47 all hash to same home location say 1 in a hash table. Then 29 will receive a 0 probe, 11 will receive a 1st probe, and 23 will receive a 2nd probe. This phenomenon is called Secondary Probing.
47. Chaining:-
Chaining involves maintaining two lists. First of all, as before, there is a table T in memory which contains the records in T, except that now, if an additional field LINK which contains the address of the next record in the chain. L may be linked together in the following manner.
Second, there is a table L called table L LIST, which contains pointers to the first record in each chain.
For example, suppose that the key K is hashed to the cell T. We place R in the T table and set the link field of R to the address of the first record in the chain. The L table contains the address of the first record in the chain at the location of linked list.
SORTING
48. Algorithm for bubble short:-
BUBBLE (DATA, N)
Here, DATA is an array of N elements. This algorithm sorts the elements of DATA.
- Step #1: Repeat step 2 and 3 for K = 1 to N – 1
- Step #2: Set PTR = 1 (Initialization of PTR)
- Step #3: Repeat while PTR <= N – k
(A) If DATA[PTR] > DATA [PTR+ 1]
Interchange DATA[PTR] and DATA[PTR+1]
(B) Set PTR = PTR + 1
[End of inner loop]
[End of step 2 outer loop]
Step #4: Exit
49. Time complexity of Bubble Sort:
(1) Best Case: Total no. of comparisons made will be decided by inner loop of 1st iteration which is n – 1.
T(n) = O(n)
(2) Average case: The comparison made is inner loop is ∑ (K-1)/2
∑(n) = n(n-1)/2 + n(n-2)/2 + … + 1/2
= n(n-1)
Tavg(n) = O(n^2)
(3) Worst case: For 1st iteration n-1 comparisons are needed for second iteration n-2 comparisons are needed.
then TBC(n) = (n-1) + (n-2) + … + 2 + 1
= n(n-1)/2
TBC(n) = O(n^2)
Space Complexity = O (1)
50. Algorithm for Selection Sort:
This algorithm uses a variable MIN to hold the current smallest value while scanning the subaray A[K] to A [N]. Specifically, first set MIN = A[K] and LOC = K, and then n-1 times, traverse the list, comparing MIN with each other element A[J].
(A) If MIN > A[K], then simply move to next element.
(B) If MIN>A[J] then update MIN and LOC by setting MIN = A[J] and LOC = J.
After comparing mean with the last element A[N] will contain the smallest among the elements A[K], A[K+1] ……A[N] and LOC will contain its location.
MIN (A, K, N, LOC)
This algorithm finds the location a LOC of the smallest element among A[K],A[K+1]…..A[N] and LOC will contain its location.
- Step 1: Set MIN = A[K], LOC = K
- Step 2: Repeat steps 3 and 4 while K <= N
If MIN > A[K], then set MIN = A[J] and LOC = J.
[End of loop]
- Step 3: return
The selection sort algorithm can now be easily used.
SELECTION (A, N)
This algorithm sorts the array A of N elements.
- Step#1: Repeat step 2 and 3 for K=1, 2, …, N-1.
- Step #2: Call MIN(A, K, N, LOC).
- Step #3: [Interchange A[K] and A[LOC]]
Set TEMP = A[K], A[K] = A[LOC], A[LOC] = TEMP.
[End of step 1 loop]
- Step #4: Exit.
51. Time complexity of Selection Sort:
1. Best Case: Total no. of comparisons will be decided by inner loop of 1st iteration which is (n-1).
T(n) = O(n^2)
2. Average case: Total no. of comparisons in inner loop is
(n-1) + (n-2) + … + 1
T(n) = O(n^2)
3. Worst case (n-1) + (n-2) + … + 1
T(n) = O(n^2)
Space Complexity = O(1)
52. Algorithm for Quick Sort:-
QUICKSORT (A, BEG, END, LOC)
Here A is an array with N elements. The parameters BEG and END contain the boundary values of the sublist of A to which the procedure applies. LOC helps to track the position of the first element A[BEG] of the sublist during the procedure. The local variables LEFT and RIGHT will contain the boundary values of elements that have not been scanned.
- Step 1: Set LEFT = BEG, RIGHT = END and LOC = BEG
- Step 2: [Scan from right to left]
(a) Repeat while A[LOC] <= A[RIGHT] and loc ≠ right
RIGHT = RIGHT – 1
[End of loop]
(b) If LOC = RIGHT, then return.
(c) If A[LOC] > A[RIGHT] then
then (i) [Interchange A[LOC] and A[RIGHT]]
Set TEMP = A[LOC], A[LOC] = A[RIGHT], A[RIGHT] = TEMP.
(ii) LOC = RIGHT.
(iii) Go to step 3.
[End of step 2 structure]
- Step 3: [Scan from left to right]
(a) Repeat while (LOC <= LEFT) loc ≠ left
Set, LEFT = LEFT + 1
[End of loop]
(b) If LOC = LEFT, then return.
(c) If A[LOC] < A[LEFT] then
(i) [Interchange A[LOC] and A[LEFT]]
Set TEMP = A[LOC], A[LOC] = A[LEFT] and A[LEFT] = TEMP.
(ii) LOC = LEFT.
(iii) Go to step 2.
[End of if structure]
53. Time Complexity of Quick Sort:
1. Best case: T(n) = O(n log n)
2. Avg case: T(n) = O(n log n)
3. Worst case: T(n) = O(n^2)
Space complexity: O(log n)
54. Stack using linklist: –
#include <stdio.h>
#include <stdlib.h>
struct node
{
int info;
struct node *link;
};
Struct node*push (struct node*);
Struct node*pop (struct node*);
Struct node*display (struct node*);
void main()
{
struct node *stop = NULL;
int info;
while(1)
{
Printf (“In push, for push, 2 for pop, 3 for display and 4 for exit”);
scanf (“%d”, &ch);
}
switch(ch)
{
case 1:
top = push(top);
break;
case 2:
top = pop(top);
break;
case 3:
display(top);
break;
case 4:
exit(0);
}
struct node *push(struct node *h)
{
struct node *p;
p = (struct node *)malloc(sizeof(struct node));
printf(“\n enter any no.”);
}
Scanf (“%d”, &p->info);
if(h == NULL)
p->link = NULL;
else
p->link = h;
return(p);
}
struct node *pop(struct node *h)
{
if(h == NULL)
printf(“\n stack is empty”);
else
{
printf(“\n the pop element is %d”, h->info);
p = h;
h = h->link;
free(p);
}
return(h);
}
void display(struct node *h)
{
struct node *p = h;
printf(“\n the stack elements are: “);
while(p != NULL)
printf(“%d”, p->info);
p = p->link;
}
Return(h);
}
55. Creation of binary tree and inorder traversal
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
struct node *create(struct node *root, int num);
void inorder(struct node *); void compare(struct node *root, int num);
struct node
{
int num;
struct node *left;
struct node *right;
};
struct node *root = NULL;
int ch;
void main()
{
int digit;
while(1)
{
printf(“enter 1 for create, enter 2 for inorder”);
scanf(“%d”, &ch);
switch(ch)
{
case 1: puts(“enter integer, enter 0 to end”);
scanf(“%d”, &digit);
while(digit != 0)
{
root = create(root, digit);
scanf(“%d”, &digit);
}
break;
case 2: puts(“inorder:”);
inorder(root);
break;
}
}
}
struct node *create(struct node *p, int digit)
{
if (p == NULL)
{
p = (struct node *)malloc(sizeof(struct node));
p->num = digit;
p->left = p->right = NULL;
}
else if (digit < p->num)
{
if (p->left == NULL)
p->left = create(p->left, digit);
else
compare(p->left, digit);
}
else
{
if (p->right == NULL)
p->right = create(p->right, digit);
else
compare(p->right, digit);
}
return p;
}
void compare(struct node *x, int digit)
{
if (digit < x->num)
{
if (x->left == NULL)
x->left = create(x->left, digit);
else
compare(x->left, digit);
}
else if (digit > x->num)
{
if (x->right == NULL)
x->right = create(x->right, digit);
else
compare(x->right, digit);
}
void inorder(struct node *p)
{
if (p != NULL)
{
inorder(p->left);
printf(“%d”, p->num);
inorder(p->right);
}
}

Leave a Reply